General idea and terminology

The ReMeta toolbox allows researchers to estimate latent parameters of observers that perform a decision-making task involving confidence ratings. Type 1 parameters refer to parameters that describe the decision-making process, while Type 2 parameters refer to parameters that describe the confidence rating process.

The focus of Remeta is an estimate of metacognitive noise, i.e. how accurately observers can monitor their own performance, and metacognitive bias, i.e. whether observers tend to be over- or under-confident.

The basic architecture of the toolbox is shown in the figure below.

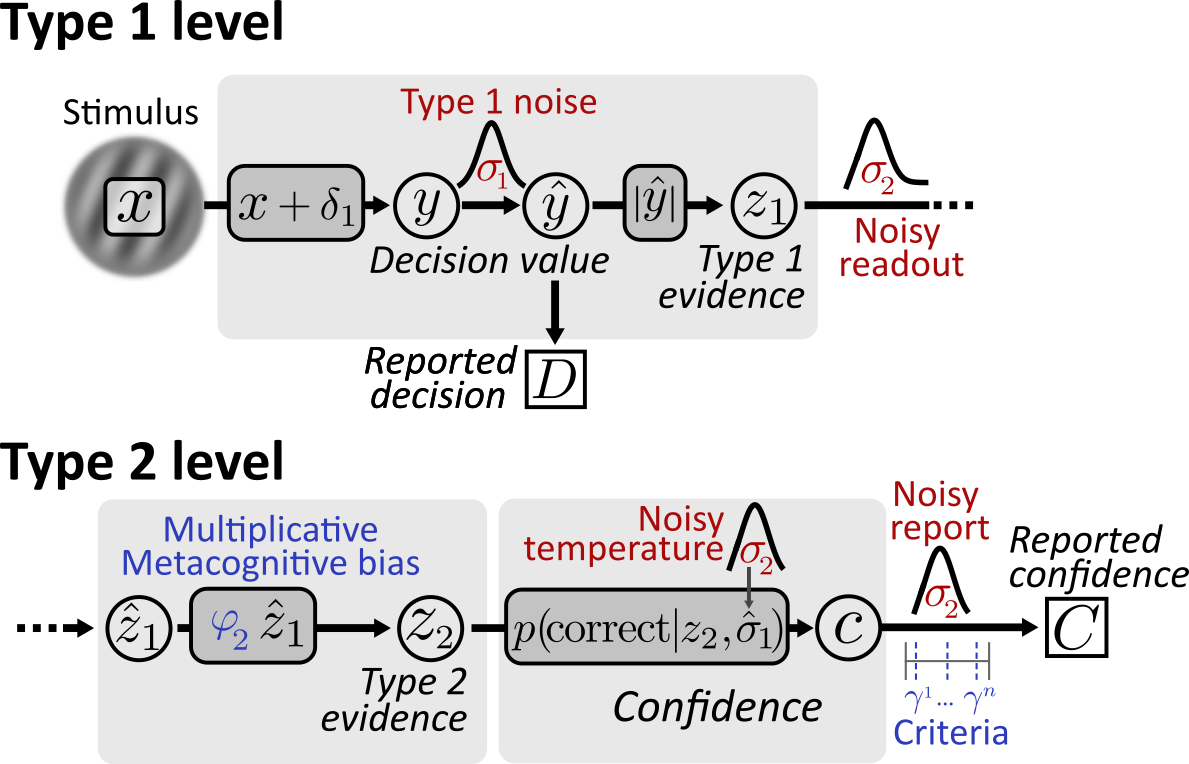
From stimulus $x$ to decisions $D$...

Based on a stimulus input $x$, the observer computes a decision value $y$, the sign of which determines a type 1 decision $D$. This process can be characterized by a variety of type 1 parameters, including type 1 noise $\sigma_{1}$ (sensory or decisional noise) and a type 1 decision bias $\delta_1$.

... from type 1 decision values $y$ to confidence ratings $C$

The absolute value of the noisy decision value — labeled type 1 evidence $z_1$ — is the relevant input to the type 2 level. It may or may not be subject to a multiplicative bias $\varphi_2$, resulting in type 2 evidence $z_2$.

By design, the model assumes that observers represent confidence as probability correct, thus computing confidence as $c=p(\text{correct}\mid z_2,\hat{\sigma}_1)$. This is sometimes referred to as Bayesian confidence1.

Finally, the mapping from an internal estimate of confidence $c$ to reported confidence $C$ is governed by a set of confidence criteria $\gamma^1, \dots, \gamma^n$.

Noise at the type 2 stage

ReMeta considers three possible sources of metacognitive noise. First, the “readout” of type 1 evidence may not be perfect, which is referred to as a noisy-readout model2.

Second, for the computation of $p(\text{correct}\mid z_2,\hat{\sigma}_1)$, the observer invariably needs an estimate $\hat{\sigma}_1$ of their own type 1 noise $\sigma_1$. This is far from trivial and may thus plausibly be subject to noise itself3. This is referred to as noisy-temperature model.

Finally, internal representations of confidence need to be communicated to the experimenter. This too is plausibly a lossy process and may inject noise into the process. This last form of metacognitive noise is referred to as a noisy-report model4.

In the figure above, all three possible sources of noise are indicated with the same parameter symbol $\sigma_2$. Not because, noise is thought to be identical, but because in ReMeta, the researcher must decide for one metacognitive noise source and hence only a single metacognitive noise parameter $\sigma_2$ will be estimated.